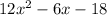1 Answer

Ladislav Ondris · Answer 1 · 2023-03-24T14:47:44+0000

Step-by-step explanation

We need to simplify this product of expressions:

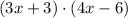
$(3x+3)\cdot(4x-6)$

We must use the distributive property of the multiplication here. We take the left expression and we multiply both terms of the right expression by it:

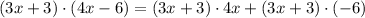
$(3x+3)\cdot(4x-6)=(3x+3)\cdot4x+(3x+3)\cdot(-6)$

Now we have the sum of two expressions. We apply the distributive property of the multiplication to both:

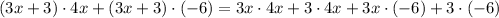
$(3x+3)\cdot4x+(3x+3)\cdot(-6)=3x\cdot4x+3\cdot4x+3x\cdot(-6)+3\cdot(-6)$

We continue operating:

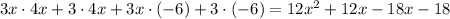
$3x\cdot4x+3\cdot4x+3x\cdot(-6)+3\cdot(-6)=12x^2+12x-18x-18$

We can use the distributive property inversely in the terms with x:

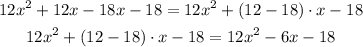
$\begin{gathered} 12x^2+12x-18x-18=12x^2+(12-18)\cdot x-18 \\ 12x^2+(12-18)\cdot x-18=12x^2-6x-18 \end{gathered}$ Answer

Then the answer is:

0 Comments

Please log in or register to add a comment.

Please log in or register to answer this question.

1 Answer

0 Comments

Please log in or register to add a comment.

Other Questions