Question

Power can also be written as force times velocity.TrueFalse

Answer 1

The work done is given as,

`W=F\cdot x\ldots(1)`

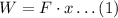
Here, F is the force and x is the displacement.

The velocity is defined as,

`\begin{gathered} v=\frac{displacement}{\text{time}} \\ =(x)/(t)\ldots(2) \end{gathered}`

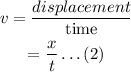
The power is defined as the rate of doing work. Mathematically,

`P=(W)/(t)`

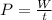
Using equation (1),

`\begin{gathered} P=(F\cdot x)/(t) \\ =F\cdot(x)/(t) \end{gathered}`

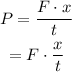
Using equation (2),

`P=F\mathrm{}v`

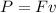
Hence, the power can also be defined as force time velocity. Therefore, the given statement is true.