Question

Can you help me with this graphthe drop down menu in the first is the same as the drop down menu in the second

Answer 1

a) the graph of y = g(x) is the graph of y = f(x) shifted horizontally up 1 unit and vertcally down 1 unit.

b) g(x) = f(x - 1) - 1

Step-by-step explanation:

a) To determine the translation done of f(x), we compare the points on both f(x) and g(x).

From the graph, we see the shape of the graph is the same size on both graphs only translation was done on f(x) to get g(x).

The Points on f(x): (-2, 1), (-1, 0), (0, 1) and (1, 0)

The correspondind points of g(x):

(-1, 0), (0, -1), (1, 0) and (2, -1)

From (-2, 1) to ( -1, 0): There is a movement of 1 unit to the right and a movement of 1 unit down

(-2 + 1, 1 -1) = (-1, 0)

From (-1, 0) to (0, -1): There is a movement of 1 unit to the right and a movement of 1 unit down

(-1 + 1, 0 - 1) = (0, -1)

from (0, 1) to (1, 0): There is a movement of 1 unit to the right and a movement of 1 unit down

(0 + 1, 1 - 1) = (1, 0)

from (1, 0) to (2, -1): There is a movement of 1 unit to the right and a movement of 1 unit down

(1+1, 0-1) = (2, -1)

`\begin{gathered} (x,\text{ y)}\rightarrow\text{ (x + 1, y - 1)} \\ x\text{ = horizontal, y = vertical} \end{gathered}`

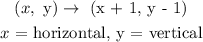
Hence, the graph of y = g(x) is the graph of y = f(x) shifted horizontally up 1 unit and vertcally down 1 unit.

b) y = f(x)

g(x): a movement of 1 unit to the right and a movement of 1 unit down

`\begin{gathered} (x,\text{ y)}\rightarrow\text{ (x + 1, y - 1)} \\ In\text{ translation: } \\ f(x\text{ + a): horizontal translation a units to the left} \\ f(x\text{ - a): horizontal translation a units to the right};\text{ }(x,\text{ y)}\rightarrow\text{ (x + a, y)} \\ f(x\text{ )+ c: vertical translation c units to the up} \\ f(x\text{ )- c: vertical translation c units to the down};\text{ }(x,\text{ y)}\rightarrow\text{ (x , y - c)} \\ \\ g(x)\text{ = }f(x\text{ - 1) - 1} \end{gathered}`