Find the inverse of A(x) = x^1/5+5

Question

asked Mar 22, 2023 120k views

1 Answer

Ajoseps · Answer 1 · 2023-03-25T22:30:29+0000

In order to find the inverse of

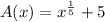
$A(x)=x^{(1)/(5)}+5$

we first replace A(x) with y:

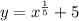
$y=x^{(1)/(5)}+5$

Then we replace every y with an x and every x with a y, like so:

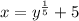
$x=y^{(1)/(5)}+5$

We solve this new equation for y:

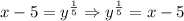
$x-5=y^{(1)/(5)}\Rightarrow y^{(1)/(5)}=x-5$

We raise both sides of the equation to the fifth power:

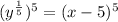
$(y^{(1)/(5)})^5=(x-5)^5$
y=(x-5)^5

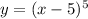
Finally, we replace y with the inverse of the function:

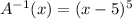
and that is the inverse function.