Question

right triangle ABC is shown on the graph below. I f the point (-4,y) lies on the line that goes through side BC of the triangle, then what should be the value of y?

Answer 1

Given:

A point (-4,y) lies on the line BC of the triangle.

The objective is to find the value of y.

Step-by-step explanation:

Consider two points of the straight line BC of the triangle ABC.

`\begin{gathered} (x_1,y_1)=(-3,2) \\ (x_2,y_2)=(0,5) \end{gathered}`

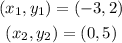
The slope of the straight line can be calculated as,

`m=(y_2-y_1)/(x_2-x_1)\text{ . . . . .(1)}`

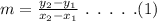
On plugging the coordinates in equation (1),

`\begin{gathered} m=(5-2)/(0-(-3)) \\ m=(3)/(3) \\ m=1 \end{gathered}`

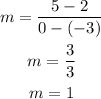
To find y:

Now, consider the given coordinate and the point C.

`\begin{gathered} (x_1,y_1)=(-3,2) \\ (x_3,y_3)=(-4,y) \end{gathered}`

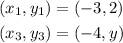
On plugging the obtained values in the equation of slope,

`\begin{gathered} 1=(y-2)/(-4-(-3)) \\ 1=(y-2)/(-4+3) \\ -4+3=y-2 \\ -1+2=y \\ y=1 \end{gathered}`

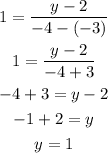
Hence, the value of y is 1.