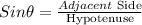The given triangle ACB is a right angle triangle with 90 degree at angle C
From the figure we have;
Angle C = 90
CB = 11.9
AC = 10
We need to find the value of angle A and the side AB
For angle Ө;
The side Adjacent to angle Ө is AC and the opposite side to angle Ө is CB
Thus., From the trigonometric ratio;
The ratio of the Opposite side to the adjacent side the tangent of the angle.
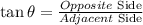
Substitute the value, Opposite side BC = 11.9 and Adjacent side AC = 10
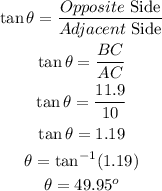
Thus, the missing angle is 49.95°
Now, for the side AB;
Apply the trignometric ratio of sin of angle 49.95°
The ratio of the adjacent side to the hypotenuse is the sine of the angle.
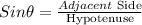
Substitute the value; Adjacent side AC = 10 and Hypotenuse AB and sin 49.95° = 0.765