The basic concept of solving a system of equations using substitution is:
- solve for one of the variables in one of the equations
- substitute this into the other equation and solve for the remaining variable
- substitute the variable you found into either equations to find the other variable.
The system of equations is:
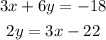
We can see that in the second equation "y" is almost solved, we just need to pass the "2" to the other side, so let's use this equations a solve for "y":
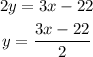
Now, we can substitute "y" into the other equations, that is, the first one:
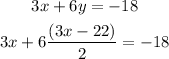
Now, the equations has only "x", so we can solve for it:
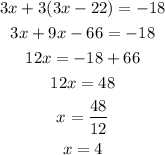
And now that we know that x = 4, we can substitute this into any of the two equations. Let's do it in the second:
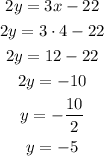
So, the solution of the given system of equations is x = 4 and y = -5.