According to the information given in the exercise:
- The number of students is 2,000.
- The driver's licenses test scores were normally distributed.
- The Mean is:
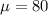
- And:
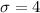
You need to know the number of students that scored higher than 88. Therefore:
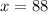
Now you can find the probability of "x" is greater than 88. This is:
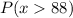
In order to calculate it, you need to approximate to a Normal Standard Distribution:
1. Remember that Z-statistic:
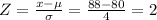
Then:
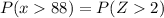
2. Now you need to use the Normal Standard Table to find:
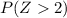
This is:
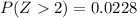
3. Therefore, you can determine that the expected number of students that scored higher than 88 is:
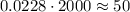
Hence, the answer is: First option.