Question

The electrical resistance of a wire varies directly as its length and inversely as the square of its diameter. (I) if a wire with aLength of 20cm and a diameter of 0.1cm has a relationship of 40ohms, determine the proportionality equation for this relationship. (I)what is the diameter of the wire if the length is 25cm and resistance is 64ohms

Answer 1

`\begin{gathered} i)R=(0.02l)/(d^2) \\ ii)0.0884cm \end{gathered}`

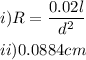
Explanations:

According to the information given;

• Let the ,electrical resistance, be "R"

,

• Let the ,length ,of the wire be "l"

,

• Let the ,diameter ,of the wire be "d"

I) If the electrical resistance (R) of a wire varies directly as its length (l) and inversely as the square of its diameter (d²), this is mathematically expressed as:

`\begin{gathered} R\alpha(l)/(d^2) \\ R=(kl)/(d^2) \end{gathered}`

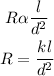
where k is the variation constant.

If a wire with a length of 20cm and a diameter of 0.1cm has a relationship of 40ohms, the proportionality equation for this relationship will be expressed as:

`\begin{gathered} R=(kl)/(d^2) \\ 40=(20k)/(0.1^2) \end{gathered}`

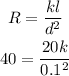
Simplify to determine the value of "k"

`\begin{gathered} 20k=40*0.1^2 \\ 20k=40*0.01 \\ 20k=0.4 \\ k=(0.4)/(20) \\ k=0.02 \end{gathered}`

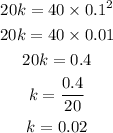
Determine the required proportionality equation for this relationship

`\begin{gathered} R=(kl)/(d^2) \\ R=(0.02l)/(d^2) \end{gathered}`

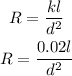
II) If the length is 25cm (l) and the resistance (R) is 64ohms, the diameter of the wire will be calculated as:

`\begin{gathered} R=(kl)/(d^2) \\ d^2=(kl)/(R) \\ d=\sqrt[]{(kl)/(R)} \end{gathered}`

Substitute the given parameters:

`\begin{gathered} d=\sqrt[]{(0.02(25))/(64)} \\ d=\sqrt[]{(0.5)/(64)} \\ d=\sqrt[]{0.0078125} \\ d\approx0.0884cm \end{gathered}`

Hence the diameter of the wire if the length is 25cm and resistance is 64ohms is approximately 0.0884cm