Question

Working with my son and need help on this question

Answer 1

To evaluate both equations using a table of values, choose the values of x and solve each equation for these x-values.

Let's choose:

x = -2.25

x = -1.75

x = 0.50

x = 0.75

Given:

`\begin{gathered} f(x)=(x-1)/(x^2+x-1) \\ \\ g(x)=3^x-2 \end{gathered}`

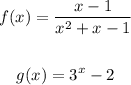
Let's substitute the values of x in each equation, solve them and compare the results using a table.

Let's begin with f(x).

`\begin{gathered} f(x)=(x-1)/(x^(2)+x-1) \\ \\ f(-2.25)=(-2.25-1)/((-2.25)^2-2.25-1)=(-3.25)/(5.06-3.25)=-1.79 \\ f(-1.75)=(-1.75-1)/((-1.75)^2-1.75-1)=(-2.75)/(3.06-2.75)=-8.87 \\ f(0.5)=(0.5-1)/((0.5)^2+0.5-1)=(-0.5)/(0.25-0.5)=2 \\ f(0.75)=(0.75-1)/((0.75)^2+0.75-1)=(-0.25)/(0.56-0.25)=-0.8 \end{gathered}`

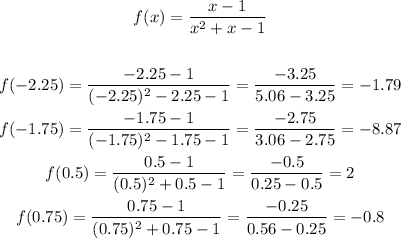
Now, let's evaluate g(x).

`\begin{gathered} g(x)=3^(x)-2 \\ g(-2.25)=3^(-2.25)-2=-1.92 \\ g(-1.75)=3^(-1.75)-2=-1.85 \\ g(0.5)=3^(0.5)-2=-0.27 \\ g(0.75)=3^(0.75)-2=0.28 \end{gathered}`

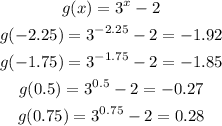
Now, let's write the results in a table to compare them.

We can observe that an aproximate solution for f(x) = g(x) is x = -2.25.

Answer: x = -2.25.