Question

A particular isotope has a half-life of 81 days. If you start with 1 kilogram of this isotope, how much will remain after 160 days? after 320 days?(Round to three decimal places as needed.)

Answer 1

Given:

A particular isotope has a​ half-life of 81 days.

Required:

If the starting amount is 1 kilogram of this​ isotope, find the remaining amount after 160 ​days, after 320 ​days.

Explanation:

The amount for exponential decay using the half line is given by the formula:

`A=P((1)/(2))^{(t)/(h)}`

Where A =accumulated amount

P = initial amount

t = elapsed time

h = half time

We have P = 1

h = 81

Find A when t = 160

`\begin{gathered} A=1((1)/(2))^{(160)/(81)} \\ A=((1)/(2))^(1.972) \\ A=0.254899 \\ A\approx0.255 \end{gathered}`

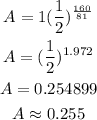
Find A when t = 320

`\begin{gathered} A=1((1)/(2))^{(320)/(81)} \\ A=((1)/(2))^(3.9506) \\ A=0.064677 \\ A\approx0.065 \end{gathered}`

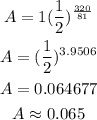
Final Answer:

The remaining amount after 160 days is approximately 0.255 kg

and after 320 days is approximately 0.065 kg.