Question

Construct the indicated confidence interval for the population mean using the t-distribution. Assume the population is normally distributed C=.95X= 13.9S= .92N= 18

Answer 1

We will answer only the first question in the first picture - as per policy.

We have a normally distributed population, and we have the following information:

• The confidence level is C = 0.95

,

• The sample mean is x-bar = 12.3

,

• The sample standard deviation is s = 3.0

,

• The sample size, n = 8

And we have to find the confidence interval for the population mean, μ, using the t-distribution.

To find it, we can proceed as follows:

1. We have that the confidence interval for the population's mean, μ, using the t-distribution is given by:

`\bar{x}\pm t^(\ast)((s)/(√(n)))`

And we already know that the sample size is less than 30 (n < 30), the population's standard deviation is unknown, and the population is normally distributed.

2. Now, we have to find the value for t^* as follows:

`\begin{gathered} t^(\ast)=(1-0.95)/(2)=0.025 \\ \\ t^(\ast)=0.025 \end{gathered}`

3. Now, we need to find the critical value for the t-distribution using the inverse cumulative function using the degrees of freedom, n - 1. In this case, n = 8. Then the degree of freedom is 7. Then the inverse cumulative function is:

`\begin{gathered} \text{ invT\lparen0.025,7\rparen=}2.36462425159 \\ \\ t^(\ast)=2.36462425159\approx2.36 \end{gathered}`

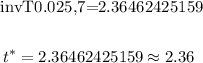
4. Now, since the t-distribution is symmetrical, then we can use the formula for the confidence interval as follows:

5. Finally, the confidence interval is:

`\begin{gathered} 12.3+2.5031580054=14.8031580054\approx14.8 \\ \\ 12.3-2.5031580054=9.7968419946\approx9.8 \\ \\ (9.8,14.8) \end{gathered}`

Therefore, in summary, the confidence interval is (9.8, 14.8).