Given:
The mass of the box is,
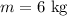
The force applied on the box is,
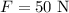
The angle of the force with the horizontal is,
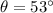
The coefficient of friction is,
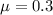
The Normal force on the box is,
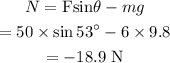
The frictional force on the box is (we take the magnitude of the force only)
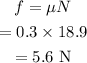
Hence the frictional force is 5.6 N.