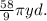Question

The circle below has center K, and Its radius is 4 yd. Given that m < LKM = 70°, find the length of the major arc LVGive an exact answer in terms of r, and be sure to include the correct unit in your answer.

Answer 1

Recall that to compute the arc length with a central angle given in degrees, we can use the following formula:

`arc\text{ length=}2\pi r((\theta)/(360)),`

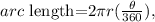
where r is the radius of the circle, and θ is the central angle.

Substituting θ = 70°, and r = 4 yd in the above formula, we get:

`\text{arclengthLKM}=2\pi(4yd)\frac{70^{}}{360}.`

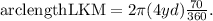
Simplifying the above result, we get:

`\text{arclengthLKM}=(14\pi)/(9)yd\text{.}`

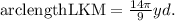
Now, to determine the arclength of LNM, first, we determine the perimeter of the circle:

`P=2\pi(4yd)=8\pi yd\text{.}`

Now we subtract the arclength of LKM and get:

`8\pi yd-(14\pi)/(9)yd=(58)/(9)\pi yd.`

Answer:

`(58)/(9)\pi yd.`