Given;
The movie aspect ratio is;
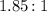
Size of the diagonal of the Televison;
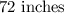
Ratio of the sides of the Television;
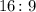
Using the ratio and a factor x we can find the width and height of the television.
The width will be;
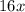
And height wil be;
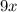
Using pythagoras theorem, since we have the value of the diagonal length of the Television;
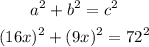
solving for x we have;
![\begin{gathered} 256x^2+81x^2=5184 \\ 337x^2=5184 \\ x^2=(5184)/(337) \\ x=\sqrt[]{(5184)/(337)} \\ x=3.922 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/fmn4jwcwed5fpv5iq37c1xff20ezfg8smc.png)
Since we have x, we can now substitute to get the width and height.
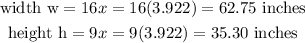
Now we can calculate the area of the Television from its width and height ;
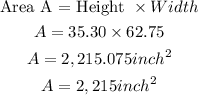
The area of the Television is 2,215 square inch
Next we need to find the Area of the image;
The height of the image is;

The width of the image will be the same as the width of the TV since the Calculated height of image is less than the height