Answer:
B and C
Step-by-step explanation:
To be able to determine all of the equations that have a = -1/2 as a solution, we'll substitute a = -1/2 into all of the equations and see which ones give us the value at the right-hand side of the equation.
A.
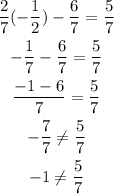
Since both sides of the equation are not equal, then a = -1/2 is not a solution of the equation.
B.

Since both sides of the equation are equal, then a = -1/2 is a solution to the equation.
C.
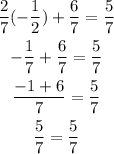
Since both sides of the equation are equal, then a = -1/2 is a solution to the equation.
D.
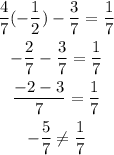
Since both sides of the equation are not equal, then a = -1/2 is not a solution of the equation.