We say that a set A is closed under an operation * if for a and b in the set
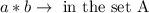
The set of integers consists of
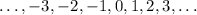
Notice that they are closed under addition, subtraction, and multiplication (the addition, subtraction, or multiplication of two integers is itself an integer).
However, as for the division,

Therefore, the set is not closed under division because the division of two integers could or could not be an integer.