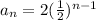The general formula for a geometric series is:

We already have our 'r' value, then, to find the coefficient we can use the term we already know.
Using the values we have in the text, we get the following relation:
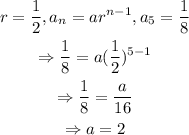
Now, we can write our general formula for the terms of this series.