Question

A 480 mL IV bag contains a 20% dextrose solution. How much of the original solution must be replaced with a 65% dextrose solution to increase the original concentration to 50%? Round your final answer to 1 decimal place if necessary.

Answer 1

320 mL

Step-by-step explanation

Let x be the amount of the 65% dextrose solution. The original solution contained 480 mL of a 20% solution and the amount x we take from that solution, is the same amount we have to add of the 65% solution to obtain the 50% concentration required.

The amount of the 20% solution left in the bag will be (480 - x). The 20% of this amount plus the 65% of x should be equal to the 50% dextrose in the final 480 mL solution. We have to solve the equation,

`0.2(480-x)+0.65x=480\cdot0.5`

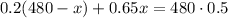
Apply the distributive property to eliminate the parenthesis and solve the product on the right side of the equation,

`\begin{gathered} 0.2\cdot480-0.2x+0.65x=480\cdot0.5 \\ \\ 96-0.2x+0.65x=240 \end{gathered}`

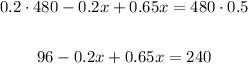
Add like terms,

`\begin{gathered} 96+(-0.2x+0.65x)=240 \\ \\ 96+0.45x=240 \end{gathered}`

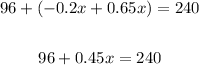
Subtract 96 from both sides,

`\begin{gathered} 96-96+0.45x=240-96 \\ 0.45x=144 \end{gathered}`

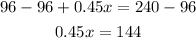
And divide both sides by 0.45,

`\begin{gathered} (0.45x)/(0.45)=(144)/(0.45) \\ \\ x=320 \end{gathered}`

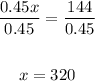
Hence, to get a 50% dextrose solution we have to replace 320 mL of the original solution with a 65% dextrose solution.