Question

A car of mass 1000 kg is heading east at 25 m/s. It collides with a car of mass 12000 kg heading north at 30 m/s. When the cars collide, they stick together. A. What is the total momentum of the system before the collision? Remember that momentum is a vector quantity, and write the momentum is component notation, with x and y unit vectors. B. What is the total momentum of the system after the collision? Write the momentum is component notation, with x and y unit vectors. C. What is the velocity of the cars after the collision? Write the velocity in component notation, with x and y unit vectors. D. At what angle do the cars move after the collision

Answer 1

We know that

• The mass of the first car is 1000 kg.

,

• The velocity is 25m/s East.

,

• The mass of the second car is 1200 kg.

,

• The velocity is 30 m/s North.

Given that there are two directions involved (East and North), we do conservation of momentum twice, one in the x-direction and one in the y-direction.

The total momentum before the collision is

`\vec{p}=m_1\cdot\vec{v}_1+m_2\cdot\vec{v}`

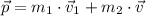
Observe that we have to use vectors.

The momentum after the collision will be

`\vec{p}=(m_1+m_2)\cdot\vec{v}_(12)`

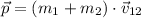
Note that after the collision, we have to add both masses and consider just one velocity because the problem indicates that the cars stick together after the collision.

According to the law of conservation of momentum, we make them equal

`m_1\cdot\vec{v}+m_2\cdot\vec{v}=(m_1+m_2)\cdot\vec{v}_(12)_{}`

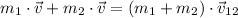
Then, we have to add the momentum vectors, the image below shows the vectorial addition

Let's write the momentum vector of each car

`\begin{gathered} p_1=m_1\cdot v_1\cdot i \\ p_2=m_2\cdot v_2\cdot j \end{gathered}`

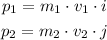
Note that "i" refers to the x-direction, and "j" refers to the y-direction. Let's use the given magnitudes.

(A) The total momentum before the collision would be

Now, we use this initial momentum vector to find the angle of the collision after the event happens.

`\begin{gathered} \theta=\tan ^(-1)((y)/(x))=\tan ^(-1)((36000)/(25000)) \\ \theta\approx55.2 \end{gathered}`

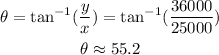
This means that the velocity after the collision has this direction of 55.2°.

Now, we have to find the module of the initial momentum vector

`|\vec{p}|=\sqrt[]{(25000)^2+(36000)^2}\approx43829.21`

Now, we use the following expression to find the velocity after the collision.

Therefore, the velocity after the collision is 16.48 m/s.

The momentum after would be

`\begin{gathered} \vec{p}=(m_1+m_2)\cdot\vec{v}_(12) \\ \vec{p}=2200\cdot(11.36i+16.36j) \end{gathered}`

At last, the car moves at an angle of 55.2° after the collision.