Question

if the city with a population of 60,000 doubles in size 90 years, what will the population be 180 years from now??

Answer 1

The process is modeled by the next formula:

`P(t)=P_0(2)^{(t)/(t2)}`

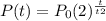
where P(t) is the population after t years, P0 is the initial population and t2 is the time needed by the population to double.

Substituting with P0 = 60,000, t = 180 years, and t2 = 90 years, we get:

`\begin{gathered} P(t)=60,000(2)^{(180)/(90)} \\ P(t)=60,000(2)^2 \\ P(t)=60,000\cdot4 \\ P(t)=240,000 \end{gathered}`

The population will be 240,000