Question

How do I graph and understand points on a graph like these

Answer 1

Option B has these points on the graph: (1, 100) and (2,50)

Explantion:

The given function:

`f(x)=100(0.5)^(x-1)`

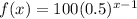
To determine which of the graph defines the function above, we will assign values for x based on the numbers given:

The values of x on the graph: 0, 1, 2, 3, 4, 5

Then we will insert the values of x in the function to see if we will get the same coordinates as any one of the graph.

let y = f(x)

when x = 1

`\begin{gathered} y=100(0.5)^(1-1)=100(0.5)^0 \\ y\text{ = 100}*1\text{ = 100} \\ (x,y)\text{ = (1, 100)} \end{gathered}`

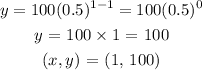
Let's pick another x point: when x = 2

`\begin{gathered} y=100(0.5)^(2-1)=100(0.5)^1 \\ y\text{ = 100(0.5) = 50} \\ (x,y)\text{ = (2, 50)} \end{gathered}`

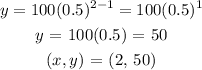
We can continue with the points to be sure. But let's check which of the graph has this points.

From the above, option B has these points: (1, 100) and (2,50)