Question

Determine whether quadrilateral ABCD is similar to quadrilateral EFGH. If so, give the similarity statement.Question options:A) Impossible to determine.B) ABCD ∼ FEHGC) The quadrilaterals are not similar.D) ABCD ∼ EFGH

Answer 1

the quadrilateral are not similar (option C)

Step-by-step explanation:

For two shapres to be similar the ratio of their corresponding sides will be equal. The angles must corresponds too.

We check if ABCD is similar to EFGH

The adjacent angles of a parallelogram sum up to 180 degree

∠A = ∠E = 80 degree

∠B = ∠F = 100 degree

∠D = ∠H = 100 degree

∠C = ∠G = 80 degree

The ratio of corresponding sides:

`(AB)/(EF)=\text{ }(BC)/(FG)\text{ =}(CD)/(GH)\text{ =}(DA)/(HE)`
`\begin{gathered} AB\text{ = 6, BC = 5, CD = 6, DA = 5} \\ EF=16,\text{ FG=24, GH=16, HE = 24} \\ (6)/(16)=(5)/(24)=(6)/(16)=(5)/(24) \\ in\text{ lowest term:} \\ (3)/(8)=(5)/(24)=(3)/(8)=(5)/(24) \end{gathered}`
`\begin{gathered} \text{From the above, we s}ee\text{ the ratios are not the same. So they are not similar} \\ \text{ABCD not similar to EFGH} \end{gathered}`

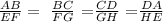
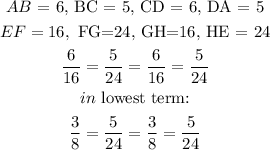
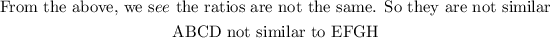
Hence, the quadrilateral are not similar (option C)