Question

In a random sample of 17 people, the mean commute time to work was 33.2minutes and the standard deviation was 7.3 minutes. Assume the population isnormally distributed and use a t-distribution to construct a 99% confidence intervalfor the population mean mu. What is the margin of error of mu? Interpret the results.

Answer 1

From the question, we are given below

`\begin{gathered} \bar{x}=mean=33.2, \\ s=\text{ standard deviation = 7.3} \\ n=\text{ sample size = 17} \end{gathered}`

Applying the confidence interval formula for t-distribution, we have

`\begin{gathered} \bar{x}\pm t*(s)/(√(n)) \\ 33.2\pm t0.99*(7.3)/(√(17)) \\ t0.99\text{ from the calculator = 2.576} \\ 33.2\pm2.576*(7.3)/(√(17)) \\ 33.2\pm4.56 \\ \backslash \end{gathered}`

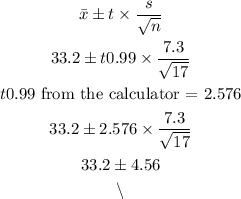
So, we have

`\begin{gathered} 33.2-4.56,33.2+4.56 \\ \left\lbrack28.64,37.76\right? \end{gathered}`

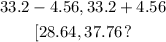
Therefore the 99% confidence interval for the population mean is:

`28.64\leq\mu\leq37.76`

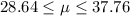
The margin of error is 4.56

There is 99% chance that the confidence interval 28.64≤μ≤37.76 contains the true population mean.