Question

The pentagons ABCDE and JKLMN are similar.Find the length x of KL.сL42.8BDKM32.1332.1J3.5NА5E

Answer 1

Given that the pentagons ABCDE and JKLMN.

Let's find the length of KL.

Given:

AB = 3

BC = 2

CD = 4

DE = 3

AE = 5

KJ = 2.1

KL = x

LM = 2.8

MN = 2.1

JN = 3.5

Since the pentagons are similar, then the corresponding sides are in proportion.

Thus, we have:

`(AB)/(KJ)=(BC)/(KL)=(CD)/(LM)=(DE)/(MN)=(AE)/(JN)`

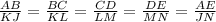
To find the value of KL, apply the proportionality equation.

We have:

`(AB)/(KJ)=(BC)/(KL)`

Input values into the equation:

`(3)/(2.1)=(2)/(x)`

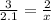
Let's solve for x.

Cross multiply:

`\begin{gathered} 3x=2*2.1 \\ \\ 3x=4.2 \end{gathered}`

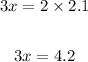
Divide both sides by 3:

`\begin{gathered} (3x)/(3)=(4.2)/(3) \\ \\ x=1.4 \end{gathered}`

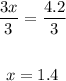
Therefore, the value length of KL is 1.4 units.

ANSWER:

x = 1.4