Question

Find the x and y intercepts of the following equation. Fill in blank one and blank two

Answer 1

`\begin{gathered} x-intercept,\:x=4 \\ y-intercept,y=2 \end{gathered}`

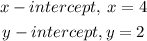
1) Since the point here is to find the x-intercept then we can plug into that equation y=0

`\begin{gathered} 4x+8y=16 \\ 4x+8(0)=16 \\ 4x=16 \\ (4x)/(4)=(16)/(4) \\ x=4 \end{gathered}`

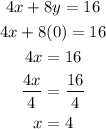
Note that when we find the x-intercept the corresponding y-coordinate is zero.

2) For the y-intercept, we'll plug into that x=0 and solve it for y:

`\begin{gathered} 4x+8y=16 \\ 4(0)+8y=16 \\ 0+8y=16 \\ 8y=16 \\ (8y)/(8)=(16)/(8) \\ y=2 \end{gathered}`

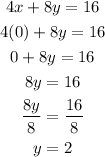
3) So the answer is x=4, y=2