Question

The weekly salaries (in dollars) for 7 employees of a small business are given below.(Note that these are already ordered from least to greatest.)538, 727, 807, 828, 900, 920, 929Suppose that the $538 salary changes to $699. Answer the following.(a) What happens to the mean?It decreases by $It increases by $It stays the same.(b) What happens to the median?It decreases by $It increases by $It stays the same.

Answer 1

(a)Mean: It increases by $23.

(b)Median: It stays the same.

Explanation:

The weekly salaries are given below:

`538,727,807,828,900,920,929`

Part A

First, we find the mean of the initial salaries:

`Mean=(538+727+807+828+900+920+929)/(7)=(5649)/(7)=807`

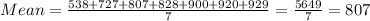
If the $538 salary changes to $699, then:

`Mean=(699+727+807+828+900+920+929)/(7)=(5810)/(7)=830`

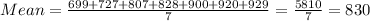
The difference = 830-807=23.

Therefore, if the $538 salary changes to $699, the mean increases by $23.

Part B

The median is the item in the middle of the data.

The initial weekly salaries are:

`\begin{gathered} 538,727,807,828,900,920,929 \\ \implies Median=828 \end{gathered}`

If the $538 salary changes to $699, the new weekly salaries are:

`\begin{gathered} 699,727,807,828,900,920,929 \\ \implies Median=828 \end{gathered}`

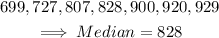
The median stays the same.