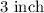Question

Ben made a scale model of the Alamo. The Alamo has an actual height of 30 feet. Ben's model used a scale in which 1 inch represents 10 feet. Which is the height in inches of Ben's model?

Answer 1

The height of Ben's model is;

`3\text{ inch}`

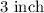
Step-by-step explanation:

Given that;

Ben's model used a scale in which 1 inch represents 10 feet

`1\text{ inch : 10 feet }`

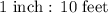
If the Alamo has an actual height of 30 feet.

`H=30\text{ feet}`

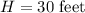
The height of Ben's model will be the actual height mutiplied by the ratio in fraction;

`\begin{gathered} h=\frac{1\text{ inch}}{\text{10 feet}}* H \\ h=\frac{1\text{ inch}}{\text{10 feet}}*30\text{ feet} \\ h=1\text{ inch }*\frac{30\text{ feet}}{10\text{ feet}} \\ h=1\text{ inch}*3 \\ h=3\text{ inch} \end{gathered}`

Therefore, the height of Ben's model is;

`3\text{ inch}`