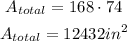Question

What is the area below?

Answer 1

`A_(total)=12432in^2`

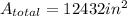
Step by step explanation:

To calculate the area of the following diagram, we can calculate separately areas for the trapezoid and the rectangle.

The area of the trapezoid is represented by the following expression:

`A=(1)/(2)(\text{ minor base+mayor base)}\cdot h`

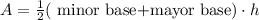
The area of the rectangle is represented by the following formula:

`A=b\cdot h`

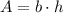
Then,

`\begin{gathered} A_(trapezoid)=(1)/(2)(13+24)\cdot4 \\ A_(trapezoid)=(1)/(2)(37)\cdot4 \\ A_(trapezoid)=18.5\cdot4=74in^2 \end{gathered}`
`\begin{gathered} A_(rec\tan gle)=24\cdot7 \\ A_(rec\tan gle)=168in^2 \end{gathered}`

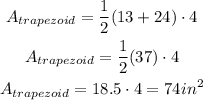
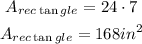
So, for the total area:

`\begin{gathered} A_(total)=168\cdot74 \\ A_(total)=12432in^2 \end{gathered}`