Question

The table of ordered pairs (x,y) (table included in picture)gives an exponential function. Write an equation for the function

Answer 1

To see what function corresponds to the table we can start by trial and error.

But we can have a hint to make it easier. We know that a number to the power of 0 will be 1. The table shows that, when x (the expoonent) is 0, we obtain a value of y = 6. This means that in the function, the number that has the x exponent should be multiplied by 6, so when it is to the power of 0 we obtain:

`6\cdot(n)^0=6\cdot1=6`

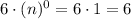
With n being any number.

With this we can say that the correct answer is the third option. Let's prove it:

When x = -1, y = 12:

`y=6\cdot((1)/(2))^(-1)=6\cdot((2)/(1))^1=6\cdot2=12^{}`

When x = 0, y = 6:

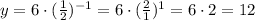
`y=6\cdot((1)/(2))^0=6\cdot1=6`

When x = 1, y = 3:

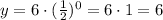
`y=6\cdot((1)/(2))^1=6\cdot(1)/(2)=(6)/(2)=3`

When x = 2, y = 3/2:

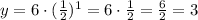
`y=6\cdot((1)/(2))^2=6\cdot(1^2)/(2^2)=6\cdot(1)/(4)=(6)/(4)=(3)/(2)`

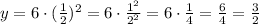
This proves the correct answer is the third option. It satisfied each point of the table.