To determine the area of the remaining paper, you have to subtract the area of the semicircle ( i.e. the area of a full circle) from the area of the rectangle.
Recall that the area of a circle is given by the following formula:

where r is the radius. Now, the semicircles have a radius of 12cm/2=6cm, therefore, the area of the circle formed by the semicircles is:
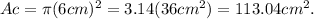
The area of a rectangle is given by the following formula:
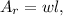
where w=width, and l=lenght. Therefore, the area of the rectangle is:
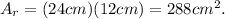
Finally, the area of the remaining paper is:
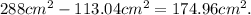
Answer:
