Draw a diagram to visualize the situation:
Notice that the vertical component of the velocity can be found using the sine trigonometric function:
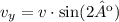
Substitute v=133.3m/s to find the vertical component of the velocity:
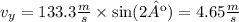
Use the formula v=d/t to find the time that it takes for the plane to descend 500m. Isolate t:

Then, the vertical component of the velocity is 4.65m/s (downwards) and it takes 107.5s to descend 500m.