Question

Find the effective annual yield and the continuous growth rate if Q=5000e^0.18t(a) The continuous growth rate is ____%(b) The effective annual rate is____%

Answer 1

INFORMATION:

If Q=5000e^0.18t we must find the effective annual yield and the continuous growth rate

STEP BY STEP EXPLANATION:

The annual yield is the return over 1 year:

- Initial investment: To find it, we need to replace t = 0 in the equation for Q

`\begin{gathered} \text{ Initial investment}=5000\cdot e^(0.18t) \\ \text{ When t = 0,} \\ \text{ Initial investment}=5000\cdot e^(0.18\cdot0)=5000 \end{gathered}`

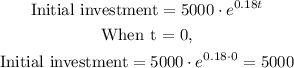
So, the initial investment is 5000

- Value after 1 year: To find it, we need to replace t = 1 in the equation for Q

`\begin{gathered} \text{ Value after 1 year}=5000\cdot e^(0.18t) \\ \text{When t=1,} \\ \text{In}\imaginaryI\text{t}\imaginaryI\text{al}\imaginaryI\text{nvestment}=5,000e^(0.18*1)=5986.0868 \end{gathered}`

Therefor the effective annual yield is

`\text{ \lparen}(5986.0868-5000)/(5000)-1)\cdot100\text{ \%}=19.7217\text{ \%}`

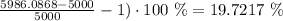
Finally, The continuous growth rate is the constant in the exponential so in this case is 0.18 or 18%

ANSWER:

(a) The continuous growth rate is 18%

(b) The effective annual rate is 19.7217%