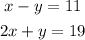
To solve a system of equations by elimination method you need to have one f the variables ( x or y) with opposite coefficient in the two equations of the system.
In this case you have the variable y with opposite coefficients; -1 and +1
You add the equations as follow:
As you get that the sum of the equations is:
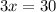
You solve the x:
- Divide both sides of the equation into 3:

You use this value of x to find the value of y by substitute the x in one of the equation by 10:

Solve for y:
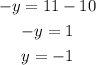
Then the solution for the system of equations is: x= 10 and y= -1