Given:
The exponential function is,
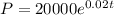
The final population is, P = 40000.
The objective is to find the correct expression to calculate the number of tears
t.
Step-by-step explanation:
Substitute the value of P in the given function.
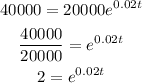
To solve the exponential function, multiiply ln on both sides of the equation.
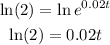
Solve for t:
On further solving the above equation,
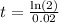
Hence, option (a) is the correct answer.