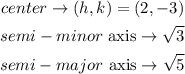Question

Looking to recieve help on this practice question, thank you!

Answer 1

In general, the standard form of an ellipse is

`\begin{gathered} \frac{(x-h){}^2}{a^2}+((y-k)^2)/(b^2)=1 \\ a,b,h,k\rightarrow\text{ constants} \\ (h,k)\rightarrow\text{ center} \end{gathered}`

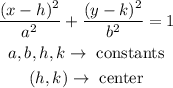
Thus, in our case, complete the squares for x and y, as shown below

`\begin{gathered} 3x^2-12x=3(x^2-4x) \\ and \\ x^2-4x+c^2=(x-c)^2 \end{gathered}`

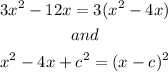
Finding c,

`\begin{gathered} \Rightarrow x^2-4x+c^2=x^2-2cx+c^2 \\ \Rightarrow-4x=-2cx \\ \Rightarrow c=2 \\ \Rightarrow3x^2-12x+3*4=3(x^2-4x+4)=3(x-2)^2 \end{gathered}`

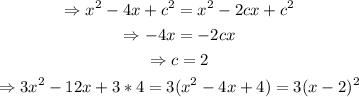
Therefore, after adding +12 to both sides of the initial equation, we get,

`\begin{gathered} 3x^2+5y^2-12x+30y+42+12=12 \\ \Rightarrow3(x-2)^2+5y^2+30y+42=12 \end{gathered}`

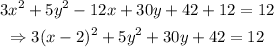
Similarly, completing the square for the variable y,

`\begin{gathered} 5y^2+30y=5(y^2+6y) \\ \Rightarrow y^2+6y+c^2=(y-c)^2 \\ \Rightarrow y^2+6y+c^2=y^2-2cy+c^2 \\ \Rightarrow6=-2c \\ \Rightarrow c=-3 \end{gathered}`

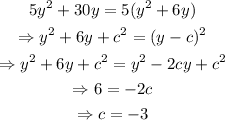
Thus,

`\begin{gathered} \Rightarrow5y^2+30y+5*(-3)^2=5(y+3)^2 \\ \Rightarrow5y^2+30y+45=5(y+3)^2 \end{gathered}`

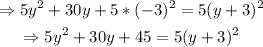
Therefore, after adding +45 to the initial expression

`\begin{gathered} \Rightarrow3(x-2)^2+5y^2+30y+42+45=12+45 \\ \Rightarrow3(x-2)^2+5(y+3)^2+42=57 \end{gathered}`

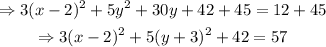
Then,

`\begin{gathered} \Rightarrow3(x-2)^2+5(y+3)^2=15 \\ \Rightarrow(3(x-2)^2)/(15)+(5(y+3)^2)/(15)=1 \\ \Rightarrow((x-2)^2)/(5)+((y+3)^2)/(3)=1 \end{gathered}`

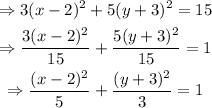
The answer is the expression immediately above this line.

The center of the ellipse, its minor axis, and major axis are

`\begin{gathered} center\rightarrow(h,k)=(2,-3) \\ semi-minor\text{ axis}\rightarrow√(3) \\ semi-major\text{ axis}\rightarrow√(5) \end{gathered}`