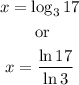To find the solution of the equation we need to remember that the logarithm functions and the exponential functions are inverse of each other that is:
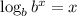
Then we apply the correct logarithm to both sides of the equation to get:
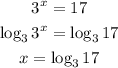
Now, if we want to write the solution in terms of the natural logarithm, we need to remember that:
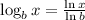
Therefore, the solution of the equation can be express in the two following ways: