Question

The angular speed for the minute hand of a clock is ___ radians/minutes.Estimate your answer using 3.14 and round your answer to the nearest hundredth.

Answer 1

To find the angular speed for the minute hand of a clock in radian/minutes

we know that,

For a minute hand, time take to complete one complete circle is 60 minutes

Distance covered by the minute hand is

`2\pi`

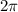
Angular speed= Distance covered/time taken

`=(2\pi)/(60)`
`=(2*3.14)/(60)`
`=0.104`

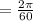
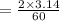
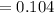
By rounding it to the nearest hundredth, we get

`=0.10`

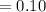
Answer is: 0.10 radian/minutes