Answer:
(-9,0)
Step-by-step explanation:
The midpoint of a line segment is the point that divides the line into two equal parts.
Given the points C(-13,-9) and D(-5,9), we find the midpoint of CD below:
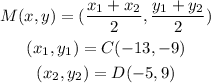
Substitution of the points C and D into the midpoint formula above gives:
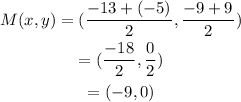
The midpoint of the line segment joining points C and D is (-9,0).