Question

18) Solve the problem. 18) y varies directly as x and inversely as the square of z. y = 108 when x = 81 and z = 3. Find y when x = 44 and z = 2 A) 26.07 B) 88 C) 264 D) 132

Answer 1

We are given that y varies directly as x and inversely as the square of z

Mathematically, the relationship is given by

`y=k(x)/(z^2)`

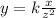
Where k is the constant of proportionality.

Let us first find the value of k

It is given that y = 108 when x = 81 and z = 3

`\begin{gathered} y=k(x)/(z^2) \\ 108=k(81)/(3^2) \\ 108=k(81)/(9)^{} \\ 108=k\cdot9^{} \\ k=(108)/(9) \\ k=12 \end{gathered}`

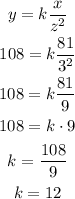
So, the value of constant k is 12

Find y when x = 44 and z = 2

`\begin{gathered} y=12(x)/(z^2) \\ y=12(44)/(2^2) \\ y=12(44)/(4)^{} \\ y=12(11) \\ y=132 \end{gathered}`

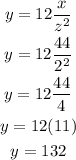
Therefore, the value of y is 132

Option D is the correct answer.