Question

if you draw two spades on the two consecutive draws with replacement from standard deck of cards you win $23. otherwise pay me $5. find the expected values of the proposition. Round your answer to two decimal places. Losses must be expressed as negative values.

Answer 1

Given a deck of card, the sample space (T) is 52, there 13 spades (S), therefore the probability of drawing two spades on two cosecutive draws is given below

`\begin{gathered} n(T)=52 \\ n(S)=13 \\ Pr(S)=(13)/(52)=(1)/(4) \\ \text{ Since there is replacement} \\ Pr(S)\text{ and Pr(S) =}(1)/(4)*(1)/(4)=(1)/(16) \end{gathered}`

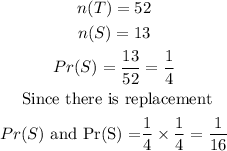
The probability of not picking two consecutive spades will be

`\begin{gathered} Pr(S_1S_2)^(\prime)=1-Pr(S_1S_2) \\ =1-(1)/(16)=(15)/(16) \end{gathered}`

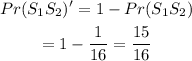
The expected value for drawing two consecutive spades will be

`\begin{gathered} ExpectedValue=xP(x)_{} \\ x=23,P(x)=(1)/(16)_{} \\ ExpectedValue=23*(1)/(16)=(23)/(16)=1.44 \end{gathered}`

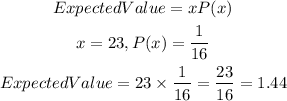
The expected value for not drawing two consecutive spades will be