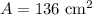Question

The surface area of a right rectangular prism is 2f + 2t + 2r, where fis thearea of the front face, t is the area of the top face, and r is the area of theright side face. Show how to use the expression to find the surface areaof4 cmthe right rectangular prism at the right. Show your work.

Answer 1

We are given the following formula for the surface area of a prism:

`A=2f+2t+2r`

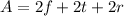
"f" is the area of the front face, in this case, the front face is a rectangle, the area of a rectangle is given by the product of its base and its height. For the front face rectangle, its base is 8cm and its height is 4 cm, therefore, "f" is equal to:

Now, for "t", the area of the top face, is also a rectangle with a base of 8 cm and a height of 3 cm, therefore its area is:

For "r", we have a base of 3cm and a height of 4cm, therefore, the area is:

Replacing in the formula for the area of the prism, we get:

`\begin{gathered} A=2f+2t+2r \\ A=2(32\text{ cm}^2)+2(24\text{ cm}^2)+2(12\text{ cm}^2) \end{gathered}`

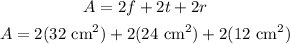
Solving the operations in the parenthesis, we get:

`A=64+48+24`

Solving the sum

`A=136\text{ cm}^2`