We are given the following two equations.
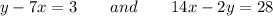
We are asked to find out whether these equations of lines are parallel, perpendicular, or neither.
First of all, let us re-write these equations into the standard slope-intercept form.
This simply means to separate the y variable.
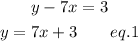
Similarly, for the other equation
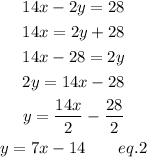
Now recall that the standard slope-intercept form is given by

Where m is the slope and b is the y-intercept.
Comparing the standard form with our two equations we see that
Slope of 1st equation = 7
Slope of 2nd equation = 7
So the two equations have an equal slope.
Whenever two equations have equal slopes then the lines are parallel.
Therefore, the given equations are parallel.