In a quadratic equation like:
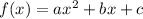
To find the vertex use the next formula:
x-coordinate of the vertex:
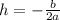
y-coordinate of the vertex evaluate the equation for x=h
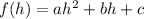
To find the zeros or x-intercepts. Equal the function to zero and solve x.
To find the Y-intercept evaluate the equation for x=0
-----------------------------------------------
For the given equations:
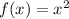
Vertex:

y intercept is 0 (coordinates (0,0))
Zeros: in (0,0)
![\begin{gathered} f(x)=0 \\ x^2=0 \\ x=\sqrt[]{0} \\ x=0 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/tmrlk5cigxyj0czkt4jfz4v7olryu11j7h.png)
-------------------------------------
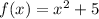
Vertex:

y-intercpet is 5 (coordinates (0,5)
Zeros:
![\begin{gathered} f(x)=0 \\ x^2+5=0 \\ x^2=-5 \\ x=\sqrt[]{-5} \\ \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/wkkvcyjnh95v3n8wngtwm0z93bwfeep95t.png)
As the square root of a negative number is not a real number the function has not zeros (doesn't cross the x-axis)