Question

Sketch the graph y = |x + 1 | + |x - 1|

Answer 1

The graph of the given absolute value function y = |x + 1 + |x - 1| is shown below:

Step-by-step explanation:

To sketch the graph, we need a couple of points on the graph. To get the points, we can replace the "x" variable in the function with any value and solve for y.

For example, x = 1.

`\begin{gathered} y=|1+1|+|1-1| \\ y=|2|+|0| \\ y=2 \end{gathered}`

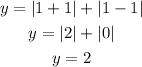
At x = 1, y = 2. Hence, we have a point at (1, 2) on the graph.

Let's try x = 0.

`\begin{gathered} y=|0+1|+|0-1| \\ y=|1|+|-1| \\ y=1+1 \\ y=2 \end{gathered}`

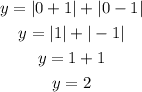
At x = 0, y = 2. Hence, we also have a point (0, 2) on the graph.

By replacing "x" with -4, 4, 2, and -2, we are able to get the points (-4, 8), (4, 8), (2, 4), and (-2, 4) and was able to sketch the graph of the function.