The formula to calculate the midpoint between two points is given by
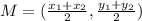
we have
M(-19,18)
(x1,y1)=(-13,15)
substitute given coordinates
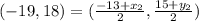
step 1
Find out the value of the x2 -coordinate
we have the equation
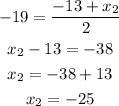
step 2
Find out the value of the y2-coordinate
we have the equation
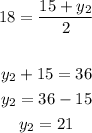
therefore
The coordinates of the other endpoint are (-25,21)