You have the following equation:

In order to solve the previous equation for x, proceed as follow:
- write 1/8 as 8⁻¹ and simplify exponents:
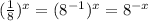
Then, the equation becomes:
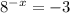
next, use properties of logarithms to obtain x. In this case apply log with base 8 to cancel 8, as follow:
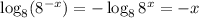
and the equation becomes:
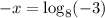
Then, you obtain log_8 (-3). Due to logarithms of negative numbers do not exist, then, the equation does not have solution for x.
Hence, in both (a) and (b) cases you have:
The solution is the empty set