EXPLANATION
Let's consider the facts:
Success rate= 9% = 0.09 (in decimal form)
Number of advertised people = 500
So, n=500, p=0.09 and 1-p=0.91
By definition, we know that:
Mean = np = 500*0.09 = 45
Now, we need to find the standard deviation:
![SD=\sigma=\sqrt[]{np(1-p)}=\sqrt[]{500\cdot0.09\cdot0.91}=\sqrt[]{40.95}=6.399218\equiv6.4](https://img.qammunity.org/2023/formulas/mathematics/college/apufxu7pvmqe7jqab73zprvnhpir3eazhv.png)
So the Probability of getting fewer than 38 sales is given by the following relationship:
P(X<38):
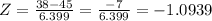
Look up z= -1.0939 on a z-table.
The obtained value is z= 0.13786 or %13.786
This means that there is a %13.78 of fewer than 38 sales.