Question

34. MAT scores are approximately normally distributed with a mean of 547 and a standard deviation of 95. Estimate the percentage of scores that were (a) between 262 and 832. % (b) above 737. % (c) below 262. % (d) between 262 and 737. %Answer (b) and (d)

Answer 1

(b) The percentage of scores above 737 can be written as follows:

`P(x>737)`

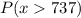
But, to find out its value, we need to first convert it to z-score, which we can do by using the mean, μ, and the standard deviation, σ:

`\begin{gathered} z=(x-\mu)/(\sigma) \\ z=(737-547)/(95)=2 \end{gathered}`

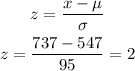
So, both are equivalents

`P(x>737)=P(z>2)`

The percentage for z-scores can be found in a z-score table, and they are given for values below a certain z. We want the percentage above a certain z, which is the same as the remainder needed to get to 1, that is, 100%.

So:

`P(x>737)=P(z>2)=1-P(z<2)`

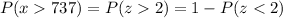
Consulting a z-score table, we see that:

`P(z<2)\approx0.977`

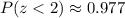
Thus:

`P(x>737)=1-P(z<2)\approx1-0.9772=0.0228=2.28\%`

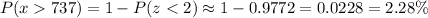
(d) To find the percentage between 262 and 737, we will need first to convert both into z:

`\begin{gathered} z_(262)=(262-547)/(95)=-3 \\ z_(737)=(737-547)/(95)=2 \end{gathered}`

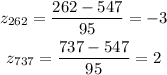
But, we also need to convert the percentage between this values to percentages regarding each of them.

If we eant the percentage between them, we can see that this is the same as taking all percentage below 737 and removing the percentage below 262, so:

`P(262The value for the first term we already have:[tex]P(z<2)\approx0.9772`

But, for the second, we need to convert to a positive z-score. Since the normal distribution is symmetric with respect to the middle, that is, 0, then it follows that:

`P(z<-3)=P(z>3)=1-P(z<3)`

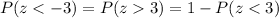
Consulting for z = 3 in the z-score table, we get:

`P(z<3)\approx0.9987`

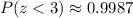
So:

[tex]P(262