Given,
The mass of the car moving east, m₁=1470 kg
The velocity of the car moving east, u₁=17.0 m/s
The mass of the car moving south, m₂=1840 kg
The velocity of the car moving south, u₂=15.0 m/s
The two components of the momentum of an object are conserved simultaneously and independently.
Let us assume that the positive x-direction is eastwards and the positive y-direction is northwards.
Thus u₂=-15.0 m/s.
Thus the vertical component of the car moving eastwards and the horizontal component of the car moving southwards are zero.
Considering the horizontal components of the momentum,
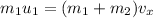
Where vₓ is the x-component of the velocity of the cars right after the collision.
On substituting the known values,
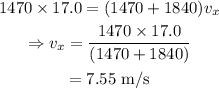
Considering the vertical components of the momentum,
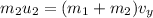
Where v_y is the y-component of the velocity of the cars right after the collision,
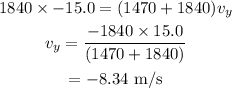
A.
The magnitude of the velocity of the cars right after the collision is given by,
![v=\sqrt[]{v^2_x+v^2_y}](https://img.qammunity.org/2023/formulas/physics/college/b1061y4obi6re8od41e46k9muims0av3n1.png)
On substituting the known values,
![\begin{gathered} v=\sqrt[]{7.55^2+(-8.34)^2} \\ =11.25\text{ m/s} \end{gathered}](https://img.qammunity.org/2023/formulas/physics/college/uwl97ulnf6uadqul1pagx3g50b1feuwxcc.png)
Thus the magnitude of the velocity of the cars right after the collision is 11.25 m/s
B.
The direction of the cars after the collision is given by,
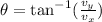
On substituting the known values,
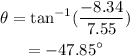
Thus the direction of the cars after the collision is -47.85°
C.
The total initial kinetic energy of the two cars is,
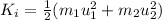
On substituting the known values,
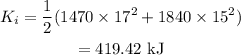
The total kinetic energy of the cars after the collision is
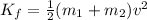
On substituting the known values,
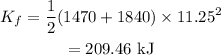
Thus the kinetic energy lost is,
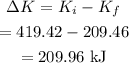
Thus 209.96 kJ of energy was converted to another form during the collision.